Энергия потока жидкости и уравнение Бернулли

Находящаяся в покое или движении жидкость обладает запасом механической энергии, то есть способностью производить работу. Полная механическая энергия потока жидкости складывается из потенциальной и кинетической энергий. Жидкость, находящаяся в состоянии покоя, обладает только потенциальной энергией. Движущаяся жидкость обладает и потенциальной, и кинетической энергией. Потенциальная энергия, в свою очередь, включает в себя потенциальную энергию положения и потенциальную энергию давления.

Таким образом, энергия потока жидкости- это механическая энергия, включающая три составляющие:

- потенциальную энергию положения;

- потенциальную энергию давления;

- кинетическую энергию.

Следует отметить, что сказанное относится к движению так называемой идеальной жидкости- жидкости, не обладающей вязкостью, в которой отсутствуют силы внутреннего трения.

Потенциальная энергия положения выражает возможность совершения жидкостью работы при ее снижении до условного уровня. Она определяется высотой потока относительно выбранной нулевой точки – точки отсчета и выделяется за счет гравитационного воздействия.

Потенциальная энергия давления выражает возможность совершения работы за счет гидростатического давления, возникающего в жидкости. Она показывает, насколько жидкость «давит», например на стенки трубопроводов. Определяется произведением веса жидкости на пьезометрическую высоту.

Кинетическая энергия жидкости зависит от скорости ее движения. Она определяется произведением веса жидкости на скоростную высоту, с которой должно свободно упасть тело, чтобы приобрести определенную скорость. Чем выше скорость потока, тем больше величина кинетической энергии.

Механическую энергию потока жидкости, отнесенную к единице веса объема, называют удельной энергией жидкости.

При рассмотрении гидравлических процессов, в частности в системах водяного пожаротушения, вместо выражения «удельная энергия» используется выражение «напор»: «удельная потенциальная энергия положения» – «геометрический напор», «удельная потенциальная энергия давления» – «пьезометрический напор», «удельная кинетическая энергия» – «скоростной напор».

Итак, рассмотрев, что представляет собой энергия потока жидкости, мы можем сформулировать широко используемое в области противопожарного водоснабжения понятие – напор. Напор – это  механическая энергия потока жидкости, протекающей через сечение в единицу времени, отнесенная к единице веса объема жидкости.

Для анализа энергии потока жидкости в различных условиях используется уравнение Бернулли – одно из важнейших уравнений гидродинамики. Уравнение Бернулли основано на законе сохранения энергии, согласно этому уравнению для установившегося потока идеальной жидкости сумма удельной потенциальной энергии положения z, удельной потенциальной энергии давления p/(ρg) и удельной кинетической энергии V²/(2g) (или сумма геометрического z, пьезометрического p/(ρg) и скоростного V²/(2g) напоров) остается постоянной в любом сечении потока z + p/(ρg) + V²/(2g) = const.

Таким образом, согласно уравнению Бернулли, при движении потока жидкости взаимосвязаны и влияют друг на друга давление, скорость и геометрическое расположение трубопровода в пространстве. То есть, если на каком то участке трубопровода изменится одна из этих величин, то изменится и другая, чтобы суммарная энергия потока оставалась постоянной. Так, если скорость потока увеличивается (например, вследствие уменьшения диаметра сечения), т.е. кинетическая энергия возрастает, то, чтобы сохранить постоянство энергии, давление уменьшится, и наоборот. Этот принцип используется, в частности, в пожаротушении, при осуществлении забора воды из водоисточников с помощью гидроэлеваторов, струйных насосов.

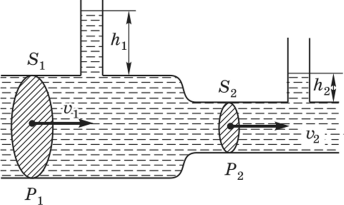
Как мы сказали, данное уравнение применимо для описания движения идеальной жидкости и, следует отметить, что при движении реальных жидкостей, обладающих вязкостью, имеет место трение, возникают потери напора h, характеризующие дополнительные затраты энергии на преодоление гидравлических сопротивлений. Уравнение Бернулли для двух произвольных сечений в этом случае выглядит следующим образом:

z₁ + p₁/(ρg) + V₁²/(2g) = z₂ + p₂/(ρg) + V₂²/(2g) + h.

При движении реальной вязкой жидкости часть механической энергии постоянно переходит в тепловую, и механическая энергия жидкости постоянно уменьшается. Эту перешедшую в тепло часть механической энергии жидкости называют потерями энергии, главным образом из-за того, что тепловая энергия в последующем уходит безвозвратно в окружающее пространство. В результате этих процессов любой движущийся поток жидкости остановится, если не компенсировать эти потери энергии внешними источниками, роль которых в противопожарных водопроводах и рукавных линиях играют, например, насосы.

О том, какие факторы влияют на величину гидравлических потерь h, возникающих при движении жидкости в системах водяного пожаротушения, мы рассказывали в статье https://portal.edufire37.ru/articles/242.